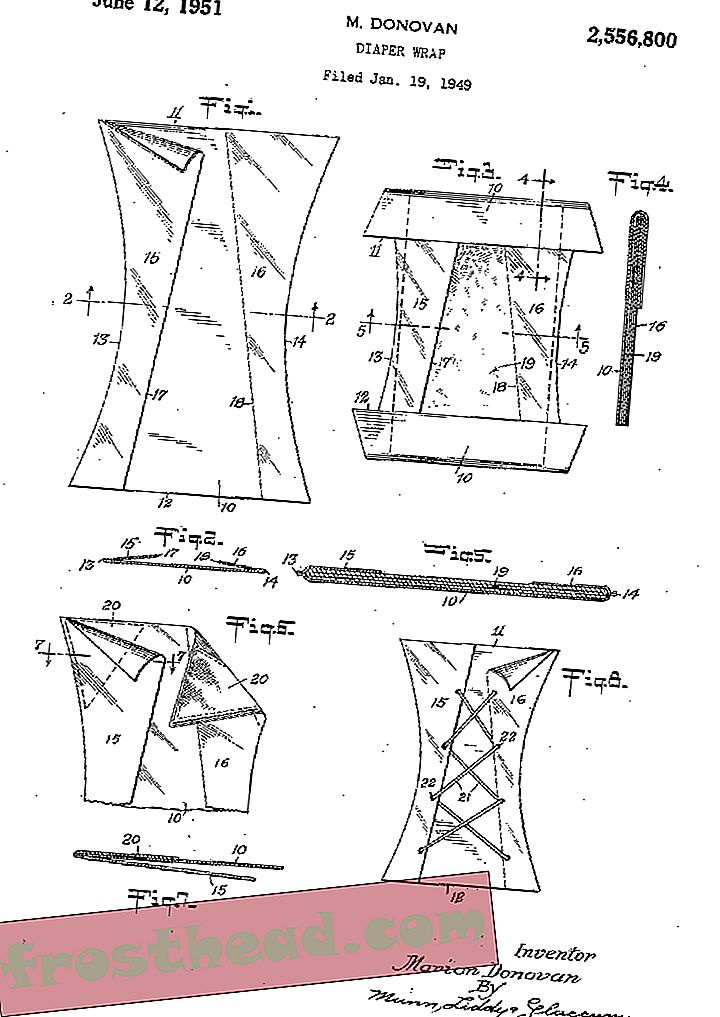
Glen Whitney staat op een punt op het aardoppervlak, het noorden breedte 40.742087, het westen lengte 73.988242, dat is nabij het centrum van Madison Square Park, in New York City. Achter hem bevindt zich het nieuwste museum van de stad, het Museum of Mathematics, dat Whitney, een voormalige handelaar in Wall Street, oprichtte en nu als uitvoerend directeur functioneert. Hij wordt geconfronteerd met een van de bezienswaardigheden van New York, het Flatiron-gebouw, dat zijn naam kreeg omdat de wigvormige vorm de mensen deed denken aan een strijkijzer. Whitney merkt op dat je vanuit dit perspectief niet kunt zien dat het gebouw, in de vorm van zijn blok, eigenlijk een rechthoekige driehoek is - een vorm die nutteloos zou zijn voor het persen van kleding - hoewel de modellen die in souvenirwinkels worden verkocht het in geïdealiseerde vorm vertegenwoordigen als een gelijkbenige, met gelijke hoeken aan de basis. Mensen willen dingen als symmetrisch zien, mijmert hij. Hij wijst naar de smalle boeg van het gebouw, waarvan de omtrek overeenkomt met de scherpe hoek waarmee Broadway Fifth Avenue kruist.
Van dit verhaal
[×] SLUITEN
Een voormalige 'algoritme manager' van het hedgefonds, Glen Whitney heeft de formule afgeleid voor het nieuwe Museum of Mathematics. (Jordan Hollender) 
Natuurkundige Steven Koonin probeert echte problemen op te lossen, zoals overmatig geluid en trage reactietijden. (Jordan Hollender) 
Terwijl de wereld steeds meer stedelijk wordt, pleit natuurkundige Geoffrey West voor het bestuderen, in plaats van stigmatiseren, stedelijke sloppenwijken. (Dan Burn-Forti / Contour door Getty Images) 
De systematische studie van steden dateert althans van de Griekse historicus Herodotus. (Illustratie door Traci Daberko) 
Fotogallerij
"De dwarsstraat hier is 23rd Street", zegt Whitney, "en als je de hoek op het punt van het gebouw meet, is deze bijna 23 graden, wat ook ongeveer de hellingshoek van de rotatie-as van de aarde is."
"Dat is opmerkelijk, " wordt hem verteld.
"Niet echt. Het is toeval. 'Hij voegt eraan toe dat twee keer per jaar, een paar weken aan weerszijden van de zomerzonnewende, de ondergaande zon direct langs de rijen genummerde straten van Manhattan schijnt, een fenomeen dat soms' Manhattanhenge 'wordt genoemd. hebben ook een speciale betekenis, behalve als nog een voorbeeld van hoe de bakstenen en stenen van de stad de principes illustreren van het hoogste product van het menselijk intellect, namelijk wiskunde.
Steden zijn bijzonder: je zou nooit een favela in Rio de Janeiro verwarren met het centrum van Los Angeles. Ze worden gevormd door hun geschiedenis en ongevallen van geografie en klimaat. Zo lopen de "oost-west" straten van Midtown Manhattan eigenlijk noordwest-zuidoost, om de Hudson en East rivieren ongeveer 90 graden te ontmoeten, terwijl in Chicago het straatrooster nauw aansluit op het echte noorden, terwijl middeleeuwse steden zoals Londen dat niet doen hebben rechthoekige roosters. Maar steden zijn ook op een diep niveau universeel: de producten van sociale, economische en fysieke principes die ruimte en tijd overstijgen. Een nieuwe wetenschap - zo nieuw dat het geen eigen tijdschrift heeft, of zelfs een afgesproken naam - onderzoekt deze wetten. We zullen het 'kwantitatieve stedelijkheid' noemen. Het is een poging om de chaotische, uitbundige, extravagante aard van een van de oudste en belangrijkste uitvindingen van de mensheid, de stad, tot wiskundige formules te herleiden.
De systematische studie van steden dateert althans van de Griekse historicus Herodotus. In het begin van de 20e eeuw ontstonden wetenschappelijke disciplines rond specifieke aspecten van stadsontwikkeling: zoneringstheorie, volksgezondheid en sanitaire voorzieningen, doorvoer en verkeerskunde. Tegen de jaren zestig gebruikten de stedenbouwkundigen Jane Jacobs en William H. Whyte New York als hun laboratorium om het straatleven van buurten te bestuderen, de wandelpatronen van voetgangers in Midtown, de manier waarop mensen zich verzamelden en in open ruimtes zaten. Maar hun oordelen waren over het algemeen esthetisch en intuïtief (hoewel Whyte, die het plein van het Seagram-gebouw fotografeerde, de stoel-van-de-broek-formule voor bankruimte in openbare ruimtes afleidde: één lineaire voet per 30 vierkante voet open ruimte). "Ze hadden fascinerende ideeën", zegt Luís Bettencourt, een onderzoeker aan het Santa Fe Institute, een denktank die beter bekend staat om zijn bijdragen aan de theoretische fysica, "maar waar is de wetenschap? Wat is de empirische basis om te beslissen wat voor soort steden we willen? ”Bettencourt, een natuurkundige, beoefent een discipline die een diepe affiniteit heeft met kwantitatief urbanisme. Beide vereisen inzicht in complexe interacties tussen grote aantallen entiteiten: de 20 miljoen mensen in het grootstedelijke gebied van New York, of de talloze subatomaire deeltjes in een nucleaire reactie.
De geboorte van dit nieuwe veld kan worden gedateerd in 2003, toen onderzoekers van SFI een workshop bijeenbrachten over manieren om aspecten van de menselijke samenleving te 'modelleren' - in de wetenschappelijke zin van herleiden tot vergelijkingen. Een van de leiders was Geoffrey West, die een netjes getrimde grijze baard heeft en een spoor van het accent van zijn geboorteplaats Somerset behoudt. Hij was ook een theoretisch fysicus, maar was afgedwaald in de biologie en onderzocht hoe de eigenschappen van organismen zich verhouden tot hun massa. Een olifant is niet alleen een grotere versie van een muis, maar veel van zijn meetbare kenmerken, zoals het metabolisme en de levensduur, worden beheerst door wiskundige wetten die op alle schaalniveaus van toepassing zijn. Hoe groter het dier, hoe langer maar hoe langzamer het leeft: een hartslag van de muis is ongeveer 500 slagen per minuut; de pols van een olifant is 28. Als je die punten in een logaritmische grafiek uitzet, waarbij grootte en pols worden vergeleken, valt elk zoogdier op of nabij dezelfde lijn. West suggereerde dat dezelfde principes zouden kunnen werken in menselijke instellingen. Aan de achterkant van de kamer betten Bettencourt (toen in het Los Alamos National Laboratory) en José Lobo, een econoom aan de Arizona State University (die in de natuurkunde studeerde als student), met het motto van natuurkundigen sinds Galileo: 'Waarom niet' krijgen we de gegevens om het te testen? '
Uit die bijeenkomst ontstond een samenwerking die het belangrijkste papier in het veld produceerde: "Groei, innovatie, schaal en het tempo van het leven in steden." In zes pagina's dicht met vergelijkingen en grafieken, West, Lobo en Bettencourt, samen met twee onderzoekers van de Technische Universiteit van Dresden legden een theorie neer over hoe steden variëren naargelang de grootte. "Wat mensen in steden doen - rijkdom creëren of elkaar vermoorden - toont een relatie met de grootte van de stad, een relatie die niet gebonden is aan één tijdperk of natie, " zegt Lobo. De relatie wordt vastgelegd door een vergelijking waarin een bepaalde parameter (bijvoorbeeld werkgelegenheid) exponentieel varieert met de bevolking. In sommige gevallen is de exponent 1, wat betekent dat alles wat wordt gemeten lineair toeneemt, met dezelfde snelheid als de populatie. Huishoudelijk water of elektrisch gebruik vertoont bijvoorbeeld dit patroon; naarmate een stad groter wordt, gebruiken haar inwoners hun apparaten niet meer. Sommige exponenten zijn groter dan 1, een relatie die wordt beschreven als 'superlinear scaling'. De meeste maten van economische activiteit vallen in deze categorie; een van de hoogste exponenten die de geleerden vonden waren voor 'private [onderzoek en ontwikkeling] werkgelegenheid', 1.34; "Nieuwe octrooien", 1, 27; en bruto binnenlands product, in een bereik van 1, 13 tot 1, 26. Als de bevolking van een stad in de loop van de tijd verdubbelt, of als een grote stad wordt vergeleken met twee steden die elk de helft kleiner zijn, is het bruto binnenlands product meer dan verdubbeld. Elk individu wordt gemiddeld 15 procent productiever. Bettencourt beschrijft het effect als "enigszins magisch", hoewel hij en zijn collega's de synergieën beginnen te begrijpen die het mogelijk maken. Fysieke nabijheid bevordert samenwerking en innovatie, wat een van de redenen is dat de nieuwe CEO van Yahoo onlangs het beleid van het bedrijf om bijna iedereen thuis te laten werken heeft omgekeerd. De gebroeders Wright konden hun eerste vliegmachines zelf bouwen in een garage, maar zo kun je geen straalvliegtuig ontwerpen.
Helaas schalen nieuwe AIDS-gevallen ook superlinearly op 1.23, net als ernstige criminaliteit, 1.16. Ten slotte vertonen sommige maatregelen een exponent van minder dan 1, wat betekent dat ze langzamer toenemen dan de bevolking. Dit zijn meestal infrastructuurmaatregelen, gekenmerkt door schaalvoordelen die het gevolg zijn van toenemende omvang en dichtheid. New York heeft bijvoorbeeld niet vier keer zoveel benzinestations nodig als Houston; benzinestations schalen op 0, 77; totale oppervlakte van wegen, 0, 83; en totale bedradingslengte in het elektriciteitsnet, 0, 87.
Opmerkelijk is dat dit fenomeen van toepassing is op steden over de hele wereld, van verschillende grootte, ongeacht hun specifieke geschiedenis, cultuur of geografie. Mumbai is anders dan Shanghai is natuurlijk anders dan Houston, maar in relatie tot hun eigen verleden en andere steden in India, China of de VS volgen ze deze wetten. "Geef me de grootte van een stad in de Verenigde Staten en ik kan je vertellen hoeveel politie het heeft, hoeveel patenten, hoeveel AIDS-gevallen, " zegt West, "net zoals je de levensduur van een zoogdier kunt berekenen op basis van lichaamsgewicht."
Een implicatie is dat, net als de olifant en de muis, "grote steden niet alleen grotere kleine steden zijn", zegt Michael Batty, die het Centre for Advanced Spatial Analysis aan University College London runt. "Als je aan steden denkt in termen van potentiële interacties [tussen individuen], krijg je daar naarmate ze groter worden meer kansen voor, wat neerkomt op een kwalitatieve verandering." Beschouw de New York Stock Exchange als een microkosmos van een metropool. In de beginjaren waren er maar weinig investeerders en handelden sporadisch, zegt Whitney. Daarom waren 'specialisten' nodig, intermediairs die een inventaris van de voorraden bij bepaalde bedrijven hielden en die een 'markt' zouden maken in de aandelen, waarbij ze de marge tussen hun verkoop- en aankoopprijs opzakten. Maar na verloop van tijd, naarmate meer deelnemers toetraden tot de markt, konden kopers en verkopers elkaar gemakkelijker vinden, en de behoefte aan specialisten - en hun winst, wat neerkwam op een kleine belasting voor alle anderen - verminderde. Er is een punt, zegt Whitney, waarop een systeem - een markt of een stad - een faseverschuiving ondergaat en zichzelf op een efficiëntere en productievere manier reorganiseert.
Whitney, die een lichte bouw en een nauwgezette manier heeft, loopt snel door Madison Square Park naar de Shake Shack, een hamburgerstandaard beroemd om zijn eten en zijn lijnen. Hij wijst op de twee servicevensters, een voor klanten die snel kunnen worden bediend, de andere voor meer gecompliceerde bestellingen. Dit onderscheid wordt ondersteund door een tak van wiskunde, de wachtlijntheorie, waarvan het fundamentele principe kan worden gesteld als: "de kortste totale wachttijd voor alle klanten wordt bereikt wanneer de persoon met de kortste verwachte wachttijd eerst wordt bediend, op voorwaarde dat de man die vier wil hamburgers met verschillende toppings worden niet razend als hij steeds naar de achterkant van de rij wordt gestuurd. "(Dit veronderstelt dat de lijn op een bepaald tijdstip sluit zodat iedereen uiteindelijk bediend wordt. De vergelijkingen kunnen niet omgaan met het concept van een oneindige wacht.) Dat idee "lijkt intuïtief", zegt Whitney, "maar het moest worden bewezen." In de echte wereld wordt de wachtlijntheorie gebruikt voor het ontwerpen van communicatienetwerken, om te beslissen welk gegevenspakket als eerste wordt verzonden.
Op het Times Square metrostation koopt Whitney een tariefkaart, in een bedrag dat hij heeft berekend om te profiteren van de bonus voor het vooruitbetalen en met een even aantal ritten te komen, zonder dat er nog geld is uitgegeven. Op het perron, terwijl passagiers heen en weer rennen tussen treinen, praat hij over de wiskunde van het gebruik van een transit-systeem. Je denkt misschien, zegt hij, dat een koerier altijd moet vertrekken zodra hij klaar is, maar er zijn momenten waarop het zinvol is om hem in het station te houden - om verbinding te maken met een inkomende local. De berekening is vereenvoudigd: vermenigvuldig het aantal personen in de sneltrein met het aantal seconden dat ze wachten terwijl het stationair loopt. Schat nu hoeveel mensen op de aankomende local zullen overstappen, en vermenigvuldig dat met de gemiddelde tijd die ze zullen besparen door de express naar hun bestemming te brengen in plaats van de local. (U zult moeten modelleren hoe ver passagiers die de moeite nemen om te schakelen gaan.) Dit kan leiden tot potentiële besparingen, in persoon-seconden, ter vergelijking. Het principe is op elke schaal hetzelfde, maar boven een bepaalde bevolkingsomvang is de investering in dubbelsporige metrolijnen of hamburgers met twee ramen zinvol. Whitney stapt in de buurt en gaat de stad in richting het museum.
***
Het is ook goed te zien dat hoe meer gegevens je hebt over transitgebruik (of hamburgerbestellingen), hoe gedetailleerder en nauwkeuriger je deze berekeningen kunt maken. Als Bettencourt en West een theoretische wetenschap van de stedenbouw bouwen, dan is Steven Koonin, de eerste directeur van het nieuw opgerichte Center for Urban Science and Progress van de New York University, van plan het voorop te zetten in de praktijk. Koonin is namelijk ook een natuurkundige, een voormalige Cal Tech-professor en assistent-secretaris van het ministerie van Energie. Hij beschrijft zijn ideale student, wanneer CUSP zijn eerste academische jaar dit najaar begint, als "iemand die hielp het Higgs-boson te vinden en nu iets met haar leven wil doen dat de samenleving beter zal maken." Koonin is een gelovige in wat soms wordt genoemd Big data, hoe groter hoe beter. Pas in het afgelopen decennium is de mogelijkheid om informatie over de beweging van mensen te verzamelen en te analyseren de omvang en complexiteit van de moderne metropool zelf ingehaald. Rond de tijd dat hij bij CUSP aan de slag ging, las Koonin een krant over de eb en vloed van de bevolking in het zakendistrict van Manhattan, op basis van een uitvoerige analyse van gepubliceerde gegevens over werkgelegenheid, doorvoer en verkeerspatronen. Het was een geweldig stuk onderzoek, zegt Koonin, maar in de toekomst zal dat niet zo zijn. "Mensen hebben de hele dag door volgapparatuur in hun zak", zegt hij. 'Ze worden mobiele telefoons genoemd. U hoeft niet te wachten tot een bureau de statistieken van twee jaar geleden publiceert. U kunt deze gegevens bijna in realtime verkrijgen, blok voor blok, uur na uur.
"We hebben de technologie verworven om vrijwel alles te weten wat er in een stedelijke samenleving gebeurt, " voegt hij eraan toe, "dus de vraag is, hoe kunnen we dat benutten om goed te doen?" De stad beter laten rennen, de beveiliging verbeteren en de particuliere sector promoten? ”Hier is een eenvoudig voorbeeld van wat Koonin in de nabije toekomst voor ogen heeft. Als u bijvoorbeeld besluit om te rijden of de metro te nemen van Brooklyn naar Yankee Stadium, kunt u een website raadplegen voor realtime gegevens over het openbaar vervoer en een andere voor verkeer. Vervolgens kunt u een keuze maken op basis van intuïtie en uw persoonlijke gevoelens over de afwegingen tussen snelheid, economie en gemak. Dit zou op zichzelf al een paar jaar geleden wonderbaarlijk hebben geleken. Stel je nu een enkele app voor die toegang zou hebben tot die gegevens (plus GPS-locaties van taxi's en bussen langs de route, camera's die de parkeerplaatsen van het stadion bewaken en Twitter-feeds van mensen die vastzitten op FDR Drive), factor in je voorkeuren en vertel je meteen: Blijf thuis en bekijk de game op tv.
Of een beetje minder eenvoudige voorbeelden van hoe Big Data kan worden gebruikt. Tijdens een lezing vorig jaar presenteerde Koonin een afbeelding van een grote strook Lower Manhattan, met de ramen van ongeveer 50.000 kantoren en appartementen. Het werd genomen met een infraroodcamera en kon dus worden gebruikt voor omgevingsbewaking, het identificeren van gebouwen of zelfs individuele eenheden die warmte lekten en energie verspilden. Een ander voorbeeld: terwijl u door de stad reist, volgt uw mobiele telefoon uw locatie en die van iedereen waarmee u in contact komt. Koonin vraagt: Hoe zou je een sms-bericht willen ontvangen met de melding dat je gisteren in een kamer was met iemand die zojuist bij de griep was ingecheckt?
***
In het Museum voor Wiskunde manipuleren kinderen en de occasionele volwassene verschillende vaste stoffen op een reeks schermen, roteren, verlengen of comprimeren of draaien ze in fantastische vormen en extruderen ze vervolgens in plastic op een 3D-printer. Ze zitten in een hoge cilinder waarvan de basis een roterend platform is en waarvan de zijkanten worden gedefinieerd door verticale snaren; terwijl ze het platform draaien, vervormt de cilinder tot een hyperboloïde, een gebogen oppervlak dat op de een of andere manier uit rechte lijnen wordt gemaakt. Of ze laten zien hoe het mogelijk is om soepel te rijden op een driewieler met vierkante wielen, als je de baan eronder contourt om de as horizontaal te houden. Geometrie, in tegenstelling tot de formele logica, wat Whitney's veld was voordat hij naar Wall Street ging, leent zich bijzonder goed voor hands-on experiment en demonstratie - hoewel er ook tentoonstellingen zijn die raken aan velden die hij identificeert als "calculus, calculus van variaties, differentiaalvergelijkingen, combinatoriek, grafentheorie, wiskundige optica, symmetrie en groepentheorie, statistiek en waarschijnlijkheid, algebra, matrixanalyse - en rekenen. ”Whitney verontrustte het dat in een wereld met musea gewijd aan ramen-noedels, buiksprekers, grasmaaiers en potloden, “ het grootste deel van de wereld heeft nog nooit de ruwe schoonheid en het avontuur gezien dat de wereld van de wiskunde is. ”Dat is wat hij wilde verhelpen.
Zoals Whitney aangeeft op de populaire wiskundetochten die hij organiseert, heeft de stad een onderscheidende geometrie, die kan worden omschreven als tweeënhalve dimensie in beslag nemen. Twee hiervan zijn die u op de kaart ziet. Hij beschrijft de halve dimensie als het netwerk van verhoogde en ondergrondse loopbruggen, wegen en tunnels die alleen toegankelijk zijn op specifieke punten, zoals de High Line, een verlaten spoorwegbok die is veranderd in een verhoogd lineair park. Deze ruimte is analoog aan een elektronische printplaat, waarin, zoals wiskundigen hebben aangetoond, bepaalde configuraties niet in een enkel vlak kunnen worden bereikt. Het bewijs is te vinden in de beroemde 'puzzel met drie hulpprogramma's', een demonstratie van de onmogelijkheid om gas, water en elektriciteit naar drie huizen te leiden zonder dat er lijnen kruisen. (Je kunt dit zelf zien door drie dozen en drie cirkels te tekenen en te proberen elke cirkel met elke doos te verbinden met negen lijnen die elkaar niet snijden.) In een printplaat moeten geleiders elkaar kruisen zonder elkaar aan te raken, soms moet verlaat het vliegtuig. Precies zo, in de stad, moet je soms omhoog of omlaag klimmen om te komen waar je naartoe gaat.
Whitney gaat uptown naar Central Park, waar hij over een pad loopt dat grotendeels langs de heuvels en hellingen loopt die zijn ontstaan door de meest recente ijstijd en verbeterd door Olmsted en Vaux. Op een bepaalde klasse van doorlopende oppervlakken - waarvan het park er één is - kunt u altijd een pad vinden dat op één niveau blijft. Vanuit verschillende punten in Midtown verschijnt en verdwijnt het Empire State Building achter de tussenliggende structuren. Dit doet denken aan een theorie die Whitney heeft over de hoogte van wolkenkrabbers. Het is duidelijk dat grote steden meer hoge gebouwen hebben dan kleine steden, maar de hoogte van het hoogste gebouw in een metropool heeft geen sterke relatie met de bevolking; op basis van een steekproef van 46 grootstedelijke gebieden over de hele wereld, heeft Whitney vastgesteld dat het de economie van de regio volgt, de vergelijking H = 134 + 0, 5 (G) benaderend, waarbij H de hoogte is van het hoogste gebouw in meters, en G is het bruto regionaal product, in miljarden dollars. Maar bouwhoogtes worden beperkt door engineering, terwijl er geen limiet is aan hoe groot een stapel je kunt verdienen met geld, dus er zijn twee zeer rijke steden waarvan de hoogste torens lager zijn dan de formule zou voorspellen. Ze zijn New York en Tokio. Zijn vergelijking heeft ook geen term voor 'nationale trots', dus er zijn een paar uitschieters in de andere richting, steden waarvan het bereik naar de hemel hun bereik van het BBP overschrijdt: Dubai, Kuala Lumpur.
Er bestaat geen stad in pure Euclidische ruimte; geometrie heeft altijd een wisselwerking met geografie en klimaat, en met sociale, economische en politieke factoren. In Sunbelt-metropolen zoals Phoenix, zijn andere dingen gelijk aan de meest wenselijke buitenwijken ten oosten van het centrum, waar je tijdens het rijden beide kanten op kunt pendelen met de zon achter je. Maar waar er een heersende wind is, is de beste plek om te wonen (of was, in het tijdperk vóór de beheersing van vervuiling) tegen de wind in het stadscentrum, wat in Londen in het westen betekent. Diepe wiskundige principes liggen ten grondslag aan zelfs schijnbaar willekeurige en historisch contingente feiten als de verdeling van de grootte van steden binnen een land. Er is meestal een grootste stad, waarvan de bevolking twee keer zo groot is als de op een na grootste en drie keer de derde grootste, en een toenemend aantal kleinere steden waarvan de grootte ook in een voorspelbaar patroon valt. Dit principe staat bekend als de wet van Zipf, die van toepassing is op een breed scala van fenomenen. (Naast andere niet-gerelateerde fenomenen, voorspelt het hoe de inkomens over de economie worden verdeeld en hoe vaak woorden in een boek voorkomen.) En de regel geldt ook al lopen individuele steden voortdurend op en neer in de ranglijst - St. Louis, Cleveland en Baltimore, een eeuw geleden allemaal in de top 10, maakten plaats voor San Diego, Houston en Phoenix.
Zoals West en zijn collega's weten, vindt dit onderzoek plaats tegen de achtergrond van een enorme demografische verschuiving, de voorspelde verplaatsing van letterlijk miljarden mensen naar steden in de ontwikkelingslanden in de komende halve eeuw. Velen van hen zullen in sloppenwijken terechtkomen - een woord dat, zonder oordeel, informele nederzettingen aan de rand van steden beschrijft, meestal bewoond door krakers met beperkte of geen overheidsdiensten. "Niemand heeft een serieuze wetenschappelijke studie van deze gemeenschappen gedaan", zegt West. “Hoeveel mensen leven in hoeveel structuren van hoeveel vierkante voet? Wat is hun economie? De gegevens die we wel hebben, van overheden, zijn vaak waardeloos. In de eerste set die we uit China kregen, rapporteerden ze geen moorden. Dus gooi je dat weg, maar wat blijf je over? '
Om die vragen te beantwoorden, is het Santa Fe Institute, met steun van de Gates Foundation, een samenwerking gestart met Slum Dwellers International, een netwerk van maatschappelijke organisaties in Kaapstad, Zuid-Afrika. Het plan is om de verzamelde gegevens van 7.000 nederzettingen in steden zoals Mumbai, Nairobi en Bangalore te analyseren en te beginnen met het ontwikkelen van een wiskundig model voor deze plaatsen, en een weg naar de integratie ervan in de moderne economie. "Lange tijd zijn beleidsmakers ervan uitgegaan dat het slecht is voor steden om steeds groter te worden", zegt Lobo. "Je hoort dingen als, 'Mexico City is gegroeid als een kanker.' Er is veel geld en moeite aan besteed om dit op te lossen, en in het algemeen is het jammerlijk mislukt. Mexico-stad is groter dan tien jaar geleden. We denken dus dat beleidsmakers zich in plaats daarvan zorgen moeten maken om die steden leefbaarder te maken. Zonder de omstandigheden op deze plaatsen te verheerlijken, denken we dat ze hier zijn om te blijven en we denken dat ze kansen bieden voor de mensen die daar wonen. "
En je kunt maar beter hopen dat hij gelijk heeft, als Batty correct is in het voorspellen dat tegen het einde van de eeuw vrijwel de hele wereldbevolking zal leven in wat neerkomt op 'een volledig wereldwijde entiteit ... waarin het onmogelijk zal zijn om elke afzonderlijke stad apart van haar buren te beschouwen ... inderdaad misschien van elke andere stad. "We zien nu, in de woorden van Bettencourt, " de laatste grote golf van verstedelijking die we op aarde zullen ervaren. "Verstedelijking gaf de wereld Athene en Parijs, maar ook de chaos van Mumbai en de armoede van Londen van Dickens. Als er een formule is om te verzekeren dat we op weg zijn naar de ene in plaats van de andere, hopen West, Koonin, Batty en hun collega's degenen te zijn die het vinden.
